| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Markov Random field
- conditional GAN
- PatchDiscriminator
- Computer Vision
- Generative model
- DCGAN
- pix2pix
- xai
- self-supervised learning
- Representation learning
- clova
- Image-to-image translation
- Gradien Vanishing
- StarGAN
- ICLR
- GAN
- Unsupervised learning
- Mutual Information
- PGGAN
- Ian GoodFellow
- Latent space
- InfoGAN
- PatchGAN
- LSGAN
- Styletransfer
- Unsupervised Representation Learning
- Today
- Total
AI with U-Seminar, Daneil Jeong
N-Beats(2020) 정리 본문
N-Beats는 시계열 데이터 예측에 사용하기 위해 새로 제안된 모델입니다.
<논문 링크>
Time Series(시계열 데이터)를 처리하기 위해 end-to-end deep learning approach를 시도한 것이 바로 N-Beats입니다.
Kaggle M4 Contest의 승자였던 ES-RNN 모델의 성능을 뛰어넘는 것이 목표로 하는데, ES-RNN에 대해서도 추후 연구해
보려고 합니다.
N-BEATS : Neural Basis Expansion Analysis for Interpretable Time Series Forecasting
1. 초록
N-Beats 모델은 인공 신경망 구조로, residual link(연결하는 원리를 의미한다, 뒤에서 다룰 것으로 예상된다)와 FC(fully-connected) layer의 깊은 적층 구조(very deep stack)로 이루어져 있다. 이 구조는 해석가능하고, 다양한 분야에서 사용될 수 있으며, 훈련 속도가 매우 빠르다. M3, M4 등에 이 모델을 실험해보았으며, 다른 기술에 비해 탁월한 성능을 보일 수 있음을 증명하였다.
2. 도입
시계열 데이터 예측은 사업적으로 중요한 문제일뿐만 아니라 ML에서도 중요한 응용사례이다. (재고 관리, 고객 관리, 마케팅, 금융 등등 다양하게 사용 가능하므로) 컴퓨터 비전이나 자연어 처리 등 이미 Deep Learning 기술이 잘 개발된 붑ㄴ야들과 달리, 시계열 데이터를 효과적으로 처리할 수 있는 모델은 여전히 연구 중에 있다. 실제로 M4 대회에서는 고전적인 방법과 ML 방법을 합친(ensemble) 모델들이 우수한 성적을 거뒀다.
M4 대회 우승자는 인공 신경망 모델(neural residual/attention dilated LSTM)에 고전적인 방법을 더한(stack with a classical Hlot-Winters statistical model)을 이용하였다. 즉, 고전적인 방법과의 결합이 예측의 정확성을 높이고 예측을 좀 더 가치있게 만들 수 있음을 알려준다. 이 논문에서는 시계열 데이터를 처리하는 순수한 Deep Learning 구조들의 가능성을 연구함으로 이러한 결론에 의문을 제기하고, 또한 신경망 구조 내부적으로 시계열 데이터 예측에 대한 해석 가능한(intepretable, 아마도 직관적으로 확인할 수 있는 특성(feature)을 추출하는(extract) 것을 목표로 하는 듯하다) 요인(factor)들을 찾는 것을 다뤄보고자 한다.
<시사점>
시계열 데이터에서 순수한 ML만으로 효과를 낼 수 있음을 보이고 싶다.
실용적으로 사용할 수 있는 해석 가능한 Deep Learning 구조를 만들고 싶다.
(고전적인 기법인 seasonality-trend-level 접근 방법과 유사하게 만들고 싶다)
3. 문제 제기
우선 이산적인 시간(discrete time, 시간이 불연속적으로 숫자로 주어진, e.g. 1일, 2일...등등)에서 단변량(univariate, 변수가 하나인)의 점예측(point forecasting)문제에 대하여 생각해보자. Forecast horizon을 H이라 하고 T의 시간동안 데이터를 관측했다고 하자. 이 때 예측하고자 하는 데이터는 T+1 부터 T+H까지의 데이터이다. T이하의 값 t를 특정 필터(정확히는 lookback window, lookback에서 알 수 있듯이 T를 기준으로 t 이전 만큼의 데이터를 입력으로 사용하겠다는 뜻)의 길이라 하자. y위에 hat이 있는 경우를 예측값이라 하면, 다음과 같이 예측의 성능을 평가할 수 있다.

이 때 m은 data의 주기성(periodicity, 예를 들어 월 데이터는 12의 주기성을 갖는다)이다.
4. N-BEATS
우선 N-BEATS의 기본 구조는 간단하고 일반적이면서 깊어야 한다(expressive, deep). 또한, feature engineering이나 input scaling에 영향을 받지 않아야 한다.(와 이건 진짜 굉장히 멋진 아이디어인 거 같다, 사실 여러번 생각해본 내용이지만 학습이 가능한 지는 의문이 들기도 한다). 즉 이러한 선행 조건들을 통해 순수한 DL으로 시계열 예측을 효과적으로 해보겠다는 뜻이다. 마지막으로, 해석 가능함을 추구하기 위해 각구조의 출력 값이 사람들이 직관적으로 알아볼 수 있게(interpretable)해야 한다.
4.1 Basic Block
아래 그림과 같은 구조를 갖는다.

가장 왼쪽에 있는 그림이 기본적인 block의 모습이다. l번째 block은 입력으로 각각 xl값을 받고, 출력으로 xl의 hat과 yl의 hat 두개의 벡터를 만든다. 모델의 가장 첫번째의 블록의 개별적인 xl은 모든 model의 입력이다(마지막 관측값까지의 모든 데이터). Input Window의 크기를 forecast horizon H의 정수배(2H ~ 7H)로 두었다. 다른 블록들의 입력 값 xl은 그 이전 블록들의 residual output(input과 block을 통과한 출력을 합친 결과)이다. y의 hat은 H의 길이를 갖는 block의 foward 예측 값 벡터이고, x의 hat은 xl 중 가장 훌륭한 예측값(backcast)이며 block이 근사된 신호에 사용될 수 있게 하였다. 내부적으로는 기본 블록은 두 부분으로 나뉜다. 첫 부분은 FC 네트워크로, foward predictors와 backward predictors를 만든다(expansion coefficient). 두번째 부분은, g 함수를 이용하여 xl과 yl을 만드는 곳이다. 아래의 식을 확인해보자.

Linear의 뜻은 간단한 선형 함수(linear projection)이다.

FC 층은 ReLU를 사용하여 non-linearity를 가진다.

이 구조는 foward expansion coefficient를 이용하여 부분적인 예측의 정확성을 높이는 것이 목적이다. 또한, backward expansion을 이용한 보조 네트워크(sub-network)을 이용하여 예측에 필요하지 않은 input의 성분을 제거하여 downstream block을 돕는다. 두번째 부분은 아래와 같이 g 함수를 이용한다.

이 때 v는 forecast와 backcast의 basis vector이다.
4.2 Doubly Residual Stacking
고전적인 residual 네트워크는 다음 층으로 넘어가기 이전에 단순히 층의 입력과 출력을 더하는 것에 그친다. DenseNet은 모든 stack과의 추가적인 연결을 통해서 이러한 원리를 확장시켰다. 이러한 접근 방법은 훈련 능력을 향상 시키는 데 큰 장점을 갖는다. 한 가지의 단점은 해석하기가 어려운 모델이라는 것인데, 이를 해결하기 위해 doubly residual stocking위에서 소개한 모델 그림의 중간이랑 오른쪽 부분)을 고안하였다. 두 개의 residual branch(줄기, 방향)을 갖고 있기 때문에(하나는 backcast prediction 하나는 forecast branch) Doubly라 명명하였다.

가장 첫번째 블록의 입력은 모델의 입력이다. 다른 block들의 경우에는 input signal의 연속적인 분석을 통해 생성된다. 이전 블록이 x hat에 해당되는 부분을 지운다.(gradient backpropagation을 할 때 효과적이다!) 각각의 블록의 출력값은 부분적인 예측 y의 hat인데, 이는 처음 stack 단계에서 합쳐진 뒤, 전체 network에 대하여 다시 한번 합계(aggregate)된다. 즉 최종적인 예측은 모든 부분적인(partial) 예측의 합이 된다. (아마 이런 부분 때문에 해석 가능하다고 한듯 한데... 모든 결과물들의 단순 합이 최종적인 결과물이므로, 각 층에서의 결과물 역시 우리가 해석 가능할 듯하다.)
4.3 Interpretability
일반적인 구조는 시계열 데이터의 특정 지식들을 기반하지 않는다.(not rely on)

이 모델을 단순히 V와 b를 학습하는 것이라 해석할 수 있다. V는 H x 세타의 차원 의 크기를 갖는 행렬이다. 즉, V의 첫번째 차원은 각각의 이산적인(discrete) 시간 영역(time domain)을 의미한다고 생각할 수 있다. V의 행(columns)의 경우에는 시간영역에서 어떠한 파동함수(waveforms)라 볼 수 있다. 이러한 파동함수를 학습하기 때문에, y는 해석 불가능하게 된다. 해석가능한 구조는 예측 모델을 분리(decomposition)함으로 알 수 있다. 예를 들어 trend와 Seasonality등. STL이나 x13-ARIMA 등등의 모델이 존재한다. NBEATS 역시 이러한 것들을 이용한다.
a. Trend Model
대표적인 특징은 단조함수이며 천천히 변하는 함수라는 것이다.

시간 벡터 t는 0에서 부터 H-1 / H 까지를 균등하게 나눈 벡터이며 각각의 예측 step을 의미한다.

이 때 T는 각 시간 벡터의 제곱들을 모아놓은 것이다.

p가 작다면(2이나 3) y는 trend를 따르게 된다(mimic)
b. Seasonality Model
시즌의 특성은 규칙적이고 순환하며, 반복되는 유동성이다.

위와 같이 간단한 Fourier Series로 표현된다. 매트릭스 형태는 다음과 같다.

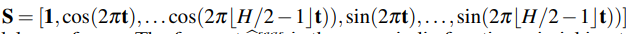
매트릭스 S는 사인파형의 행렬이다. 즉 y는 seasonal pattern을 따른다.
해석가능한 구조는 위와 같이 두개의 stack을 이용한다. forecast/backcast의 원리를 결과로 doubly stack을 만들고 이로 부터 trend 성분을 제거한 뒤, seasonality stack에 이를 넣어준다.
4.4 Ensembling
Ensembling은 시계열 예측의 핵심이다. Ensembling 기법은 dropout이나 L2-norm penalty보다 탁월한 Regularization(overfitting 방지)능력을 발휘한다. (Dropout이나 L2-norm penalty는 ensemble과 함께 사용할 수 없다) Ensemble의 가장 핵심적인 특징은 다양성이다. 우선, ensemble 모델들은 3가지의 다른 평가기준(metrics, sMAPE, MASE, MAPE)를 이용한다. 두번째로, 모든 horizon H마다(예측 시점) 각 모델들은 2H,...,7H 까지 6가지의 서로 다른 window 크기로 학습한다. 따라서, 총합한 ensemble은 다양한 크기의 aspect(multi-scale)을 갖는다. 마지막으로 baggin 방법을 사용한다.(각 model을 서로 다르게 랜덤하게 초기화한다) 180개의 각기 다른 모델을 사용하였고, ensemble을 합치기 위하여(aggregate function) 중앙값(median)을 사용하였다.
4. 관련지식
시계열 데이터를 다루는 방법은 몇몇의 항목으로 분류할 수 있다. exponential smoothing을 기반으로한 통계학적 모델링의 방법이 있을 수 있다.(Holt, Winters) 좀 더 발전된 방법으로는 M3 대회의 우승자인 Theta Method가 있다. (예측을 여러 개의 theta-line들로 나눈 뒤, 통계학적으로 합쳐준다) 이러한 방법들에는 ARIMA, auto-ARIMA 등이 있다. 최근에는 ML과의 결합을 통해 좋은 성능을 얻고 있다(통계학적인 기법을 feature로 이용한다) M4의 준우승자는 여러 통계학적 기법을 데이터 셋에 적용한뒤 gradient-based 트리를 이용하여 예측을 진행하였다. RNN을 이용하는 시계열 예측 역시 존재한다. Dilation이 있는 RNN과 resiudal connection, attentnion을 포함한 방법 역시 존재한다. 이 방법은 M4 대회 우승자의 기반이 되었다. 우승자는 Holt-Winter의 seasonality model과 dilation/residual/attentino approach를 적절히 혼합하여 예측을 진행하였다. (hybrid model)
5. 토론 (결과 부분은 생략한다)
Meta-learning은 내부(inner) 학습 과정과 외부(outer) 학습과정을 의미한다. 내부 학습 과정은 외부 학습 과정에 의해 영향을 받고, 변화한다. 예를 들어, 동물의 경우, 외부 학습은 동물 일생 동안의 개별적인 학습이며, 내부 학습은 여러 세대의 많은 개인들에 걸친 학습이다. 두 학습을 모두 확인하기 위하여, 각각 parameter를 선정해준다. (inner -> synaptic weights, outer or meta parmaeters -> genes) N-BEATS에서는 외부 학습이 전체 네트워크의 parameter들 안에 들어있다(encapsulated). 내부 학습의 경우에는 basis building block안에 존재한다. 내부 학습은 stage의 흐름에 따라 이루어진다.(매 블록마다) 메타 parameter들은 오롯이 FC 층에만 존재한다. Generic Model의 경우에는 V안에도 존재한다.
6. 결론
시계열 데이터 예측에 새로운 구조를 제안하였다. 이 모델은 일반적이고, 유연하고, 다양한 분야에서 활용 가능할 것이다. 이 DL은 시계열 예측과 관련된 배경 지식이 없어도 잘 동작할 수 있다. 또한, 사람들이 해석 가능한 결과를 보여줄 수 있다. 또한, 다양한 데이터에 대하여 학습을 진행하고 모델을 전이하거나 공유하는 것이 가능하다. 또한 메타 러닝 등에도 사용할 수 있기 때문에 향후 활용성이 높을 것으로 예상된다.
-> 사실 N-BEATS가 엄청 뛰어난 성능인지 아닌지는 잘 모르겠다. 한번 써보는 것이 좋을 거 같다.
'데이터사이언스' 카테고리의 다른 글
| Temporal Fusion Transformers(2020) (0) | 2021.05.12 |
|---|

