| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Latent space
- clova
- Representation learning
- PatchDiscriminator
- Styletransfer
- Image-to-image translation
- pix2pix
- Unsupervised Representation Learning
- conditional GAN
- Ian GoodFellow
- LSGAN
- StarGAN
- PGGAN
- self-supervised learning
- DCGAN
- xai
- Gradien Vanishing
- InfoGAN
- Unsupervised learning
- Markov Random field
- Computer Vision
- GAN
- PatchGAN
- Mutual Information
- Generative model
- ICLR
- Today
- Total
AI with U-Seminar, Daneil Jeong
Wasserstein GAN (2017), WGAN-GP 본문
1. WGAN
GAN의 가장 큰 문제점 중 하나는 불안정한 학습(unstable train)입니다.
GAN은 아래식과 같이 데이터의 분포를 학습시키는, 즉 parameter에 대하여 데이터 분포를 실제 데이터의 분포와 비슷하게 만드는 것(maximize loglikelihood)이 목표입니다. 라벨이 따로 없기 때문에 unsupervised learning의 일종이죠.
(추후에 라벨이 들어가는 conditional GAN 등이 나오긴 합니다)

그런데, P(x)는 실제로 어떠한 분포를 갖고 있는 지 알아내기 어렵습니다. GAN에서는 이를 해결하기 위해 random한 noise(latent variable) z에서 부터 원하는 분포를 찾는 과정을 거칩니다. 이 때 두 개의 적대적(adversarial) 모델 Generator와 Discriminator가 학습을 진행합니다. (통칭 G와 D 네트워크)
https://aijyh0725.tistory.com/12
Generative Adversarial Nets (2014)
GAN 논문 리뷰 첫번째입니다. 0. 배경 Generative Model은 초기 Boltzman machine으로 부터 시작하여 DBM(2009), VAE(2014)등이 등장하였습니다. Generative Model을 2개의 큰 특징으로 정의하면 아래와 같습니다...
aijyh0725.tistory.com
하지만 두 개의 네트워크의 균형을 맞추며 학습하는 것은 굉장히 어려운 일입니다. 실제 GAN에서 사용되는 objective를 이용하여 학습을 진행할 경우, 너무 빨리 포화된(saturated) D로 인해 G가 특정 mode만을 이용하는 결과를 초래할 수도 있습니다(mode collapse, or mode dropping) 즉, G가 비슷한 정보만을 이용하여 샘플을 만들어내어 D를 속이고, 이 과정에서 data distribution이 global한 데이터 분포 영역을 포함하고자 하는 목적과 달리 일부만을 표현하게 됩니다.
따라서, 새로운 GAN의 훈련 환경을 만드는 것은 당시에는 굉장히 매력적인 일이었습니다. (지금도 마찬가지 입니다)
WGAN에서는 아래와 같은 차별점을 통해 언급된 GAN의 문제점들을 해결하고자 합니다.
- Discriminator를 critic이라 명명합니다. critic은 더이상 classifier(진짜와 가짜를 구분하는)가 아닙니다.
- critic은 Lipschitz 조건을 만족해야 합니다.
- critic은 이제 EM distance로부터 도출해낸 특정 scalar 값이 됩니다.
- KL divergence는 continuous하지 않은 특징 등 때문에 학습이 불안정합니다.
새롭게 사용하게 될, EM distance based critic, 속칭 Wasserstain-1 distance를 사용한 GAN은 좋은 discriminator를 사용하여 보다 안정된 학습과 mode collapse의 문제를 해결하고자 합니다.
https://arxiv.org/abs/1701.07875v3
Wasserstein GAN
We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learning curves useful for debuggi
arxiv.org
2. Introduction
앞서 말씀드린 것과 타이, 기존의 방식은 random variable z와 parametric function을 정의하고, 가장 유사한(최대의 log likelihood를 갖는) z와 paramter의 데이터 분포를 찾는 방식이었습니다. 모델의 분포와 데이터의 분포의 차이를 다양한 방법을 통해 정의하는 데, 그 중에는 distance와 divergence 등이 존재합니다. 만약 정의된 거리가 0이 된다면 모델의 학습을 마친 것이겠죠?(converge) 이러한 distance는 또한 weak topology여야 합니다. weak topology의 정의는 구글에 검색해보면 아래와 같이 나옵니다.
" X->Y로 보내는 모든 함수 f_a들이 모두 연속함수가 되게 하는 최소한의 topology"
topology는 위상 수학에서 사용되는 위상의 개념입니다. 저희가 흔히 배우는 거리의 성질은 흔히 traingle inequality라 불리는 피타고라스의 정리라 알려진 개념을 따릅니다. 즉, 두 원소 사이의 거리가 다른 원소를 거쳐서 갈 때보다 항상 작아야 한다는 삼각부등식의 정리를 따릅니다. 위상수학은 이와 다르게 거리공간의 개념을 열린 집합을 이용하여 정의합니다. 위상 수학에 대한 자세한 개념은 아래 블로그를 확인하시면 좋을 거 같습니다.
https://jjycjnmath.tistory.com/150
위상수학이란 무엇일까?
위상수학은 무엇을 공부하는 학문일까? 오늘은 위상수학(topology)에 대한 일반적인 얘기로 시작해 보려고 한다. 우리가 흔히 학부 수준에서 접하는 위상수학은 사실 일반위상수학(general topology)
jjycjnmath.tistory.com
앞서 데이터의 분포가 연속적이어야 했었는 데, 그 중에서도 데이터의 분포의 convergence는 distance가 결정하게 됩니다. 만약 distance가 weaker topology라면, continuous mapping을 정의하는 것이 더욱 쉬워져서 분포가 더 잘 converge 될 것입니다.
weaker distance -> easy distribution convergence -> easy continuous mapping
따라서, loss fucntion은 거리를 통해 정의하여, 이를 최적화시킴으로 converge한 분포를 찾을 것입니다.
어떠한 것들이 distance의 후보가 될 수 있을까요?
a. TV distance (Total Variation)

b. KL Divergence (Kullback-Lebiler)
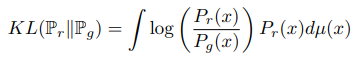
위 두개는 두 데이터 분포 사이의 기본적인 distance와 divergence가 됩니다.
c. JS divergence (Jensen-Shannon)

d. EM distance (Earth-Mover, Wasserstein-1)
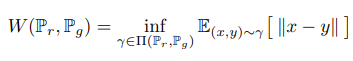
EM distance는 두 개의 데이터 분포에 대한 모든 joint distribution에 대하여, 한 데이터를 다른 데이터로 옮기는 데 필요한 mass를 구합니다. EM distance는 이러한 계획(transport plan)에 필요한 최소(optimal) 경비(cost)가 됩니다.
다른 3가지와 EM distance의 차이를 알아보기 위해, convergence를 예시로 듭니다.
우선 uniform distribtuion을 갖는 Z와, 이를 통해 구성된 P0 = (0,Z)를 통해 convergence를 확인해봅시다.

EM distance(맨 위 W)를 제외한 다른 모든 function들은 0에서 continuous하지 않습니다. 즉, 세타 값이 0으로 갈 때 diverge하게 됩니다. 이를 통해 low dimensional manifold에서 EM distance만이 gradient descent를 통해 학습이 가능한 것을 알 수 있습니다 (나머지는 모두 divergen 하기 때문에 불가능)
WGAN은 이러한 원리와 Kantorovich-Rubinstein duality를 이용하여 W를 다음과 같이 봅니다. 이 때 f는 Lipschitz function(정확히는 1)입니다.

WGAN은 훈련 과정에서, K-Lipschitz한 성질을 만족시키기 위해 weight을 clipping시켜줍니다.
(물론 clipping은 좋은 방법이 아니라 논문에서도 주장합니다. 예를 들어 cliiping이 너무 크다면 critic이 학습을 하는 데 걸리는 시간이 길어지게 되고, 너무 작다면 vanishing gradient 등의 문제를 겪을 수 있다 합니다)
WGAN은 아래와 같이 훈련을 진행합니다. 특별히 RMSProp을 사용하였는 데, Adam등은 momentum을 사용하기 때문에 학습이 불안정하다고 합니다.

2. WGAN-GP
WGAN-GP는 WGAN의 훈련을 개선하기 위해 나온 논문입니다. 그 중에서도 언급했던 K-Lipschitz 조건을 만족시키기 위해 사용하였던 불안정한 방법인 clipping 대신 새로운 방법론을 제시합니다. (gradient penalize)
https://arxiv.org/abs/1704.00028v3
Improved Training of Wasserstein GANs
Generative Adversarial Networks (GANs) are powerful generative models, but suffer from training instability. The recently proposed Wasserstein GAN (WGAN) makes progress toward stable training of GANs, but sometimes can still generate only low-quality sampl
arxiv.org
굉장히 좋은 논문이라 NIPS에 나오기도 하였습니다. WGAN은 아래와 같은 value function을 갖습니다.

critic의 weight이 compact space [-c, c]에 있게 하여 Lipschitz constraint를 만족하게 하기 위해 clipping을 사용하지만, 이와 같은 방식은 불안정하다 WGAN에서도 언급하였습니다. WGAN의 이와 같은 방법은 아래와 같은 두 가지 문제점을 갖고 있습니다.
- 데이터 분포의 강한 모멘트를 clipping 때문에 훈련 과정에서 무시하게 된다
- exploding & vanishing gradient
WGAN은 gradient penality 아이디어를 통해 이를 극복하고자 합니다. 만약에 differentiable 함수가, 즉 gradient의 norm이 전부 1에 가깝게 한다면 1-Lipschitz를 만족하게 될 것입니다. 미분 가능성을 해결하기 위해(tractability issue) 아래와 같이 soft한 방식의 grdient norm penalty를 제시합니다.

이와 같은 GP 방식은 더이상 Bacth normalization을 사용하지 않게 됩니다. 각각의 input에 대하여 critic의 gradient norm을 penalize해주기 때문에 entire batch에 대한 방식은 필요없어지게 됩니다. 오히려 layer normalization등의 방식을 향후 연구에 추천합니다.
gradient norm은 two-sided하게 penalty를 줍니다. 무슨 소리냐면, 1보다 작은 값과 큰 값 모두 1에 가깝게 되는 것을 의미합니다. 예를 들어 1보다 작게만 하는 것은 1-sided이겠죠?

WGAN과 GP를 통해 불안정한 학습을 해결하고, mode collapse 역시 어느 정도 해결하였습니다. 이제 이러한 WGAN의 방식을 다양한 모델 구조에도 적용하는 것이 추후 연구 과제일 것입니다. 혹은 scaling이 큰 이미지 데이터셋에 대해서도 학습이 일어날 수 있을 것입니다(학습이 안정적이기 떄문에!) GP 방식은 discriminator가 smoothing한 decisino boundary를 학습하는 것에도 굉장한 도움을 주었습니다. 굉장히 직관적이면서도 효과적인 방법론입니다.
* 사설
굉장히 어려운 논문이었습니다. 수학적 지식이 부족함을 많이 느꼈네요 ㅎㅎ
'GAN' 카테고리의 다른 글
| Pix2Pix(PatchGAN, 2016) (0) | 2022.04.23 |
|---|---|
| LSGAN (2016) (0) | 2022.04.22 |
| InfoGAN (2016) (0) | 2022.04.18 |
| DCGAN (2015) (0) | 2022.04.15 |
| Generative Adversarial Nets (2014) (0) | 2022.04.14 |




