| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- conditional GAN
- InfoGAN
- self-supervised learning
- Mutual Information
- GAN
- ICLR
- Unsupervised learning
- Computer Vision
- PGGAN
- Latent space
- PatchGAN
- Styletransfer
- xai
- Image-to-image translation
- clova
- DCGAN
- Ian GoodFellow
- LSGAN
- pix2pix
- Unsupervised Representation Learning
- Gradien Vanishing
- PatchDiscriminator
- StarGAN
- Markov Random field
- Generative model
- Representation learning
- Today
- Total
AI with U-Seminar, Daneil Jeong
LSGAN (2016) 본문
GAN의 학습은 굉장히 불안정합니다. GAN의 학습 불안정 중, 특정 샘플에 대하여 gradient vanishing 문제가 발생하는 경우가 있습니다. Discriminator의 decision boundary (real과 fake를 구분하는)에서 멀리 떨어져 있는 fake sample에 대하여, gradient가 너무 작아 훈련이 제대로 일어나지 않습니다. 즉, fake sample을 decision boundary에 가깝게 만들어 real sample가 구분하기 어렵기 하고 싶은데 그것이 잘 일어나지 않게 됩니다.
논문에 나온 아래 그림을 보겠습니다.
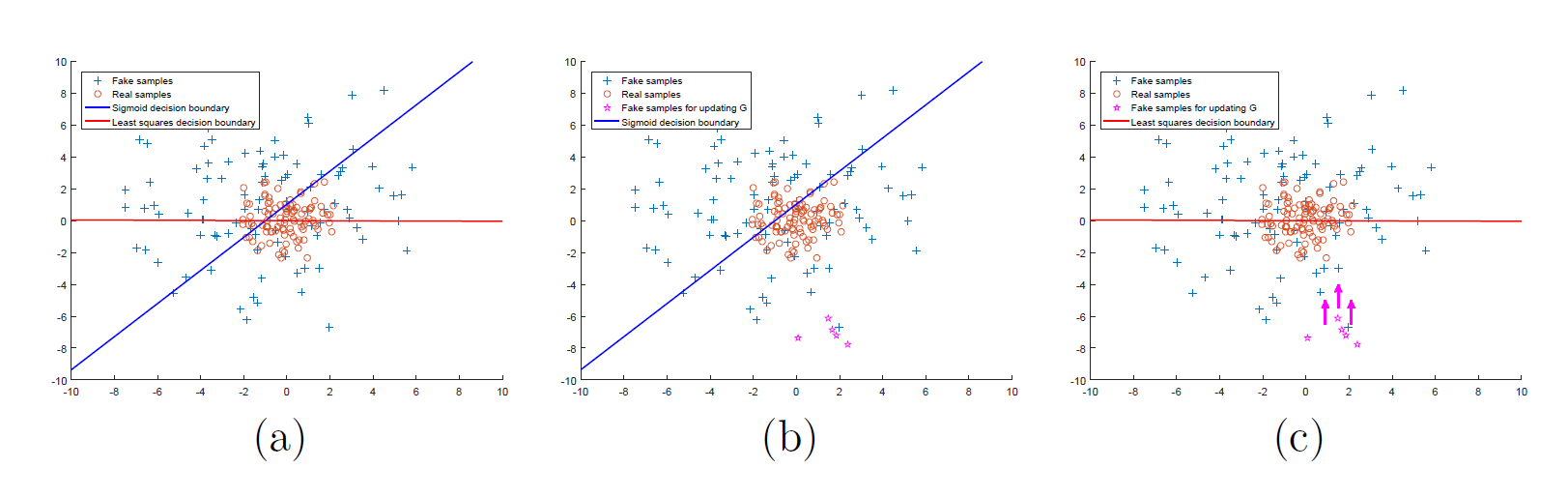
각 그래프에 파란색 선은 sigmoid의 decision boundary를 의미합니다. 주황색 선은 논문에서 사용된 기법인 least square이 적용된 decision boundary입니다. b에서 추가된 별표의 fake sample들은 decision boundary에서 멀리 떨어져 있는, correct class에 속해있는 sample들입니다. 이들을 Discriminator에 집어넣어 얻은 결과의 gradient는 너무 작기 때문에 Generator를 충분히 학습시키는 데 어렵습니다. 그런데, 만약 Least square 방식을 사용하면 어떨까요? 즉, decision boundary와의 거리를 반영하여 gradient를 계산한다면, 멀리 있는 sample들을 boundary 주변으로 끌어당기는 데 효과적일 것입니다.
LSGAN의 목표는 새로운 loss function을 통해 GAN의 훈련을 안정화시키고, 좋은 품질의 이미지를 생성하는 것입니다.
https://arxiv.org/abs/1611.04076v3
Least Squares Generative Adversarial Networks
Unsupervised learning with generative adversarial networks (GANs) has proven hugely successful. Regular GANs hypothesize the discriminator as a classifier with the sigmoid cross entropy loss function. However, we found that this loss function may lead to t
arxiv.org
1. 논문리뷰
GAN은 unsupervised learning에서 좋은 representation을 학습하는 데 효과적인 모델입니다. GAN 모델은 end-to-end하게 differentiable하기 때문에 approximate 등도 사용하지 않습니다. 그러나 앞서 설명드린 것처럼 GAN의 불안정한 훈련(unstable train)이라는 단점을 갖습니다. 그 중에서도 LSGAN은 Generator 학습에 있어서 gradient vanishing이 일어나는 것에 주목합니다. 만약, 특정 기준을 세우고 그 지점까지의 least square한 loss를 구하게 discriminator를 만든다면, decision boundary와의 거리 때문에 생기는 문제점을 해결할 수 있을 것입니다.
논문의 기여는 다음과 같이 정의됩니다.
- LSGAN은 Pearson divergence를 최소화하는 방법론입니다
- 좋은 품질의 이미지를 만들고, 안정적인 학습을 추구합니다
기존 GAN의 Discriminator는 sigmoid cross entropy loss를 이용하여 fake(0)와 real(1)을 구분하였습니다. 즉, classifier의 역할을 하고 있는 셈이죠. 아래는 그러한 loss function과 least square loss function에 대한 비교입니다.

sigmoid가 x의 값이 커질 수록 loss값이 0에 가깝게 saturation이 일어나 gradient에 문제가 일어나는 것과 달리,
least square의 경우 특정 지점에서만 0이 되고, 그 외에는 거리에 quadratic하게 반응하는 것을 알 수 있습니다.
만약 a를 fake data의 라벨, b를 real data의 라벨, c를 G가 D를 속이는 라벨이라 한다면,
아래와 같은 식을 세울 수 있습니다.

Least square 형태의 loss fucntion이 두 개가 만들어지게 됩니다. 즉, decision boundary와의 거리 값을 기준으로(square하게 만들어준 이유), 그 거리 값에 비례하여 loss를 구성하여 멀리 떨어져있을 수록 더 많이 gradient를 계산하게 하는 것이 목적입니다.
LSGAN의 식을 자세히 보면, 잘 분류된 sample들 역시도 decision boundary에 멀리 있을 경우 큰 gradient를 갖게 penalize 시켜줍니다. 이 때, G를 잘 업데이트 하기 위해 거리를 계산하므로, D를 freeze하여 decision boundary는 가만히 둡니다. 좋은 decision boundary는 실제 데이터의 manifold를 가로 질러야 하는데, 생성되는 모든 샘플들을 decision boundary로 보냄으로 인해 생성된 샘플의 분포가 실제 데이터의 분포와 가까워지게 만듭니다.
LSGAN의 loss function에 optimal한 Discriminator를 가정하여 식을 푸면 아래와 같이 됩니다.

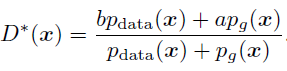

맨 아래식은 Pearson divergence의 형태로, 데이터의 분포와 생성된 데이터의 분포 사이의 divergence를 나타내기 됩니다. 정확히는 데이터의 분포 + 생성 데이터의 분포 와 2 * 생성 데이터의 분포 사이의 divergence를 나타내는 데, objective function을 최소화하는 것은 결국 이 pearson divergence를 최소화하는 것이 됩니다.
또한 LSGAN은 GAN의 문제점 중 하나인 mode collapse도 해결합니다.
아래 그림은 gaussian dataset에 대한 실험으로, Gaussian kernel density estimation을 한 결과입니다.

기존 GAN이 15k의 step부터 한 mode만 생성하는 것과 달리, LSGAN은 다양한 mode를 잘 만들어내는 것을 확인할 수 있습니다. 아마도 decision boundary에 근접한 data 숫자가 많아져서, mode를 다양하게 만들어낼 가능성이 높아진 거 같습니다. 다만, 그러한 방법론이 mode의 다양성을 100 % 보장한다고 생각하진 않습니다.
'GAN' 카테고리의 다른 글
| CycleGAN(2017) (0) | 2022.04.24 |
|---|---|
| Pix2Pix(PatchGAN, 2016) (0) | 2022.04.23 |
| Wasserstein GAN (2017), WGAN-GP (0) | 2022.04.21 |
| InfoGAN (2016) (0) | 2022.04.18 |
| DCGAN (2015) (0) | 2022.04.15 |




